中学受験算数「速さ」克服ガイド｜きはじ・旅人算・進行グラフまで一気に整理
中学入試の「速さ」攻略ガイド：三公式・単位換算・図の描き方を固めよう
中学入試の算数では、「速さ」の問題がほぼ確実に出題されます。
速さそのものの考え方や比を使った解法に加え、旅人算・流水算・通過算・時計算・ダイヤグラム・つるかめ算など、さまざまな文章題が一つの単元に集中しているのが特徴です。
その一方で、多くのお子さんが
- 速さ・距離・時間の3用法があいまい
- 単位換算（時速・分速・秒速）がスムーズにできない
- 文章を読んでも状況がイメージできない
といったつまずきを抱えたまま、旅人算やダイヤグラムといった応用に入ってしまい、「速さ＝苦手分野」になりがちです。
このページでは、速さの単元の中でもとくに大切な「基本計算」と「考え方」を整理し、どのように克服していけばよいかを解説します。
動画講義：速さの三公式と「きはじ」の考え方
まずは動画で、速さの三公式と基本的な考え方を確認してみてください。
１．速さという単元の全体像と「3用法」
速さの単元に含まれる多くの要素
速さという単元には、いろいろな要素が組み合わさっています。
速さそのものの考え方や、比を使った解法に加え、
- 旅人算
- 流水算
- 通過算
- 時計算
- ダイヤグラム など
複数のジャンルの文章題が一つにまとまっているのが速さの特徴です。
塾によって多少前後しますが、速さを最初に学ぶのは4年生の後半〜5年生の前半が多く、このタイミングでまず学ぶのが
「距離・速さ・時間」の関係です。
たとえば、
- 距離と速さが分かれば時間が求められる
- 時間と速さが分かれば距離が求められる
といった内容です。ここでしっかり定着させたいのが、次の3用法です。
速さの三公式（3用法）と「きはじ」
速さの三公式（3用法）は次の通りです。
- 距離 ＝ 速さ × 時間
- 速さ ＝ 距離 ÷ 時間
- 時間 ＝ 距離 ÷ 速さ
これを覚えやすくするために、よく使われるのが「きはじ」という方法です。
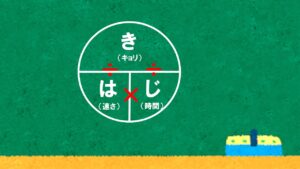
「きはじ」のイメージは次の通りです。
- き：距離
- は：速さ
- じ：時間
円や三角形の中に「き・は・じ」を配置し、求めたい文字を隠すことで式をつくる方法です。
- 時間を求めるとき：時間を隠して「距離 ÷ 速さ」
- 距離を求めるとき：距離を隠して「速さ × 時間」
「きはじ」が落とし穴になることもある
たとえば、
「20mを1分で進むことができる人が、100m進むには何分かかるか？」
という問題は、本来なら
- 100 ÷ 20 ＝ 5（分）
と、割り算ですぐに出せます。
しかし、公式を丸暗記していると、
- 「どの公式を使うんだっけ？」
- 「きはじの図をまず描いて…」
と、かえって時間がかかってしまうことがあります。
速さが得意な生徒ほど、「きはじ」を使う方が逆に時間がかかると感じます。
問題を見た瞬間に何算か判断できるのに、わざわざ図を書いている時間が無駄になるからです。処理に時間がかかるほど、ほかのことを考えられなくなり、問題の違和感やひっかけにも気づきにくくなってしまいます。
3用法は「一瞬で判断して一瞬で式に移る」
3用法は、
一瞬で判断して、一瞬で式に移れる
必要があります。
「きはじ」で考えている間はどうしても処理が遅れ、他に注意が向けられなくなります。したがって、3用法は
無意識でできるレベル（問題を見て2秒以内に式が書けるレベル）
にしておくことが望ましいのです。
２．単位の違う計算と単位換算のコツ
よくあるつまずき：時速と分の組み合わせ
次のハードルが、単位の違う計算です。
例：「時速30kmで12分進むと何kmか？」
本来は掛け算で求める問題ですが、
30 × 12 といきなり計算しようとしてしまったり、単位をそろえずにそのまま計算してしまうことがよくあります。これは4年生だけでなく、5・6年生でもつまずく典型例です。
単位変換には2つのパターンがある
単位変換の考え方には、次のようなパターンがあります。
（１）速さを分速や秒速に直す
例：時速30km → 分速500m
時速30kmを分速に直してから12倍する、という方法です。
（２）時間を「時間」に直す
例：12分 → 12 ÷ 60 ＝ 12/60時間
そのうえで、
- 30 × 12/60
と計算すれば距離が求められます。
「分を見た瞬間に分母に60を書く」反射をつくる
このとき重要なのは、
分を見た瞬間に分母に60を書く
という反射です。
理屈を考えながら「12分は何時間だったかな…」と考えていると時間がかかり、その間に自分が何をしていたか忘れてしまうこともあります。
だったら最初から、
- 12/60時間
と書けるようにしておく方が効率的です。
基本計算があいまいなままだと、応用問題は解けない
このような計算が素早くできるようになることで、速さ・距離・時間を自由に扱えるようになります。
速さの単元が苦手な生徒の共通点は、ほとんどの場合、
ここ（基本計算）があいまいなまま
進んでいることです。
たとえば、
「300mを分速150mで進むと何分？」
という基本問題でも、
- 「割るんだっけ？ 掛けるんだっけ？」
と迷ってしまう状態では、旅人算や流水算ができなくなるのは当然です。
つまり、基本が固まっているというのは、
割り算を分数に直すことが無意識でできる
ということです。
考えなくても手が動くレベルまで落とし込むことが大切です。速さの単元ができるかどうかは、こういった「基本処理の精度」がカギになります。
夏井算数塾の『オンライン個別指導』：通塾せずに教室と同じ授業を受講できます
中学入試の算数で速さの問題が得意になるには？
中学入試の算数で出題されることの多い「速さ」の問題を苦手とされる方を多く目にします。速さの問題を得意にしておくことで、中学入試で出題された場合も安心して問題に取り組めるようになります。
苦手を克服したいからといって、やみくもに色々なことに手をつけてしまっては中途半端になってしまいます。まずは苦手の原因を見つけ、順を追ってひとつずつクリアしていきましょう。
１．速さの単位を正しく理解する
単位時間あたりで進むきょり（時速・分速・秒速など）、速さの単位を理解できていないと速さの問題を解くことはできません。また、単位換算もスピーディーにできるようにしておく必要があります。
これらがきちんと理解できていないと、
- 車と徒歩でどちらが早く着くかを比べたはずなのに、徒歩の方が速いという計算になってしまった
といった、答えが明らかにおかしい場合でも、それに気づくことができません。
速さの三公式を覚えて、使いこなせるようにしていきましょう。
２．単位を書く習慣をつける
特に中学入試で出題される速さの問題を解いていると、途中で何を求めていたのか分からなくなってしまう場合があります。
計算式のすべてに単位を書く必要はありませんが、
- ひとつ答えが出たら、その数字の横に単位を書く
- 長い計算の後には、必ず単位を書く
といったように、何を求めていたのかを見失わないために、単位を書き入れるクセをつけるようにしましょう。
単位の間違いで、せっかく計算で正解の数字が出せている問題が不正解や減点になってしまうことがないように、ケアレスミスにも注意が必要です。
３．問題の条件を正しく把握する
中学入試で出題される速さの問題は、
- 途中で速さが変わる
- 出発する時間が異なる
- 途中で休憩をはさむ
など、状況が複雑になっているものが多くなります。
文章だけではイメージしづらくても、見やすい形に整理してしまえば案外解きやすい問題だったということもよくあります。
式だけでは解きにくい場合は、図やグラフなどを書いて状況を整理することで、ぐっと解きやすくなります。
４．図やグラフをかいて状況を見える化する
問題を図に表す際には、
- 文章を読んで分かったことを、最初から順番に書き出す
- 示されている条件はすべて図に書き入れる
ようにしましょう。
そして、図にしたあとで、その図が正しいかどうかを再度文章と照らし合わせて確認します。せっかく図を描いたのに、そもそもの読み取りを間違えていると、勘違いに気づかずに最後まで解き進めてしまいかねません。
自分が目で見て分かりやすい形を見つけるためにも、さまざまなパターンの問題で図やグラフを書く練習が必要です。
５．特に注意したい問題：ダイヤグラム・旅人算
中でも、ダイヤグラムや旅人算は速さの問題の中でも難しい分野です。速さや比、距離や時間などさまざまな内容が問題に含まれており、情報整理が非常に難しく感じてしまうかもしれません。
ダイヤグラムや旅人算の問題では、特に図やグラフに表すことが大切です。図やグラフに表すと、
- 文章以外の情報も目に入りやすくなる
- 設定が頭の中でイメージしやすくなる
ため、解きやすくなります。
速さの問題の条件を正しく把握するために、特にダイヤグラムや旅人算では意識して図やグラフをかくようにしましょう。
６．「つるかめ算」を使う速さの問題
速さの問題で、途中で速さが変わるというパターンがあります。
このような問題では、面積図をかいてつるかめ算を用いると、図と式の両方で考えることができ、効率よく解くことができます。
一見つるかめ算の問題ではないように見えても、
- 実はつるかめ算を使うことで簡単に解ける問題だった
というパターンは少なくありません。問題演習の数をこなし、「つるかめ算を使うべきかどうか」を見極められるようにしていきましょう。
７．比や逆比を活用する
速さは、比や逆比を用いて計算するパターンが多くあります。比を用いる場合は、文章で書かれている内容を正しく読み取り、どの量どうしが比例・反比例の関係にあるのかを整理します。
解法が複数ある場合でも、比や逆比を用いることで計算が大幅に簡単になることがあります。
比や逆比をうまく用いて、計算の時間を短縮していきましょう。
８．まとめ：速さの問題に強くなるために
中学入試の算数において「速さ」の問題は頻出で、まったく出題されないということはほとんどありません。難関校になればなるほど、条件が複雑だったり、文章だけでは理解するのが難しくなっていきます。
速さの問題を得意にするためには、
- 速さの三公式・単位換算といった基礎部分をきちんと覚える
- そのうえで、図やグラフで状況を正しくイメージできるようにする
- 旅人算・ダイヤグラム・つるかめ算・比や逆比など、応用パターンに少しずつ慣れていく
ことが大切です。
旅人算やダイヤグラムの問題では難しい問題も多いため、最初はなかなか解けず、苦手意識を持ってしまうこともあるかと思います。しかし、慣れてくれば難しい問題も徐々に解けるようになります。
単位換算や速さの公式の活用などは、特にコツコツ毎日問題を解き、手が勝手に動くレベルまで慣れることが大切です。
当塾での取り組み
当塾では完全個別の１対１授業で、速さの問題の苦手克服のための授業が受講できます。
当塾の授業の独自のシステムについては、夏井算数塾・個別指導はココが違う！をご覧ください。
また、教室での授業と同様の授業をオンラインでも受講可能です。通塾の必要がなく、全国どこからでも勉強し慣れた環境で受講でき、勉強だけに集中して取り組むことができます。
詳細は今までにない、“業界初”のオンライン算数個別指導「ウィズ・ユー」をご覧ください。
