中学受験における算数で文章題の正答率を上げるためのポイント
今回は単元別のコツという事で、つるかめ算のお話をしておこうと思います。
つるかめ算自体は、いわゆる文章題の中でも二番目に登場します。
多分一番が和差算だと思いますが、二番目にたくさん登場する色んな問題でもよく使う文章題になっています。
なので、当然やった事がある生徒さんも多いでしょうし、色々パターンも結構多いので、それをしっかりと勉強しなきゃいけないという事になります。
大きな特徴としては、色んな解き方があるという事です。
例えばシンプルな問題一つとっても結構色んな解き方が出来るというお話になっています。
という事で、例えばですが、50円切手と、最近あまり見かけないですが、80円切手というものがあって、合計20枚用意しました。
それぞれが何枚かは分かりませんが、とりあえず合計20枚あるんだという事になっていて、その合計金額が1240円だったとしましょう。
この時、50円切手とか80円切手の枚数は何枚あるんでしょうね？というのを考えましょうというのがいわゆるつるかめ算と言われる文章題になります。
色んな解き方があるというお話を先ほどしましたが、ざっくり有名なものだけ上げておいても、例えば5パターンぐらいあります。
もちろんメジャーというか、皆使うよね、というやつからあんまり見た事がないやつと結構差はあったりしますが、一つ一つ見ておきましょう。
一番多いのは面積図で教えてもらうという事が多いんじゃないかなと思います。
どういう面積かと言いますと、お金を面積で表わすという表現の仕方をします。
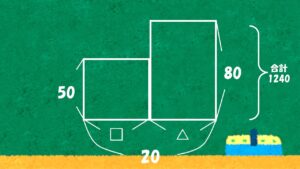
50円切手だから縦50円にしておきましょう。
横何枚か分かりませんのでとりあえず□と書いておきましょう。
80円切手の方も同じです。
80円切手も枚数何枚か分かりません。
そうすると、この面積というものがお金、金額の合計を表しているという事になっています。
これがいわゆる面積図解法と言われるものになります。
合計が1240円だと分かっているという事になるので、まず分かる事は合計の枚数が20枚という事は最初から知っている訳です。
ここの枚数を足してあげると20枚という事になっていますので、どこか面積が分かる場所ないかな？という事を考える訳です。
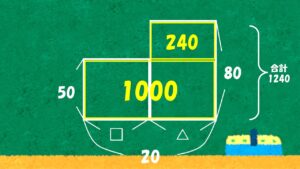
考えると、例えばこの下の部分ならいくらか、と計算出来るはず。
縦が50で横が20だと書いていますから、ここを計算すると1000円になる、という事が分かるという事になります。
という事は、合計1240円と分かっている訳なので、この上側の面積は240だという事が分かるという事になります。
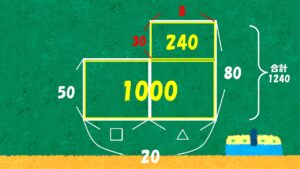
そうすると、あとはこの縦の長さに注目しましょう。
ここからここまでは80円と50円の違いになっているので、ここが30円だという事が分かりますので、ここは240÷30で8枚だという事が分かります。
という事で、80円切手の枚数は8枚です。
50円の枚数は20から8を引いてあげれば12枚になるよね、という事が分かるという感じで答えを求める事が出来るというのがいわゆる面積図を使った時のつるかめ算の解き方という事になります。
これを面接図を使わずとも解けるよね、という話をしているのが二つ目です。
全体の差を1あたりの差で割ってあげましょうという事を考えます、という事です。
言葉で説明すると長々になるのでちょっとざっくりお話しをしていくだけで終わらせたいんですが
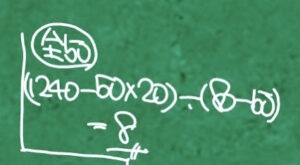
まず一つ目、例えば80円切手の枚数を求めたいんだとすると、何を考えればいいかというと、取り敢えず80円切手を求めたい場合、反対側、つまり全部50円切手だと思いましょう。
もし全部が50円切手だったら、という所からスタートします。
これを私はよく全50と表現したりします。
もし全部が50円切手だったら訳して、全50という事です。
もし全部が50円切手の場合、もちろん50円切手が20枚ある訳ですから50×20で1000円にしかなりません。
実際1240円と言っているのでだいぶ話が違うな、となります。
差を求めてあげると、これが240円です。
全体の差が240という事になる訳です。
じゃあ今度は÷1あたりの差です。
要は、どれだけ嘘付いたからこうなったのかというと、80円のものまで50円と言ってしまったからこうなった、つまり80円50円から1枚あたりの嘘は30円という事になります。
という訳で、全体の差を1あたりの差で割ってあげると枚数が出ます。
240÷30だから確かに8枚と答えが求められます。
さっきの答えと一緒です。
これも8枚でした。
という感じで答えを求める事が出来るという事になります。
あとは表解というものもあります。
同じ問題でいきますが、今度はこれを表にして書いていきましょうというのもよく出てくる話です。
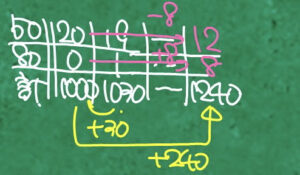
50円切手、80円切手という事で、それぞれ何枚ずつあるかは今の所分からない訳です。
分からないのでとりあえず全部君たちは50円切手というふうにしてしまいましょう。
つまり、20枚0枚の場合から考えましょうというのをやる訳です。
そうすると合計金額が何円になるんですか？という事を計算すればいいです。
50×20は1000です。
80×0は0です。
合計すると1000円だという事がこれで分かったという事になりました。
でも合計は1240円だと分かっているんだからこれは違うな、という事が分かります。
じゃあ1回交換してみましょう。
19枚、1枚の場合何円になるんだろうか、という事を考える訳です。
そうすると、50円19枚で950円。
80円1枚で80円。
950+80で1030円という事が分かるね、という事になっています。
という訳で、ちょっとずつ金額が変わっていくんだなという事が分かります。
今回の目的はなんだったかと言いますと、今回は1240円が合計金額になればいいんだよ、という話をした訳です。
という事になるのでどうなればいいかというと、1回交換するごとに30円ずつ増えているので、全部を交換する為に240円増えるという事は何回交換すればいいのか？というのは割り算で求める事が出来ます。
240÷30だから8回交換すればいいんだ、という事が分かりました。
8回交換するという事は、こっちは8減るはずだし、こっちは8増えるはずだよね、という事になるので、上は20-8で12枚、下は0+8で8枚というふうにして答えが求まるという感じで枚数を求めてあげましょうというのが表解を使った面積図の解き方という事になります。
あと、てんびんはちょっと置いておいて状況図です。
状況図はなんの事なんですか？というと、多分どこかで見た事あるかも知れませんが、こんな解き方になります。
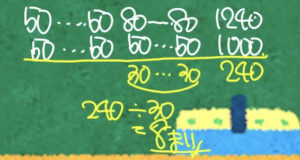
今50円切手と80円切手が何枚かずつあって合計二十枚だと言っており、そして合計金額は1240円だという事が分かっているという事までは知っている訳です。
やる事はさっきと一緒です。
もし全部が50円だったらという事を考えます。
もし全部が50円だった場合っていうのは、もちろん20枚中20枚全部が50円な訳ですから合計金額は1000円になってしまうよね、という事になります。
そこで差に注目してあげればいいんじゃないの？というのがこの問題の解き方です。
80と50だからこっち側の差は別にないんですが、こっち側は1枚あたり30円の差が生まれています。
その結果、最終的に1240円と1000円という差になっていますから、240円の差が出来ているよね、となります。
多分、差集め算、過不足算で書くやり方と結構似ています。
という事になるので、ここは240÷30という事になる、という事でもともと80円切手だったものが8枚あるんだ、という事が分かればいいという事になっているという感じで答えを求める事が出来るというのがいわゆる状況図を使ったつるかめ算という事になります。
ただ、今四つの解き方を聞いてもらってなんとなく分かった人もいるかも知れませんが、実は出てくる数字全部一緒です。
実は計算する事は何も変わらないんですが、表現の仕方が違う、というふうになっているのがつるかめ算の解き方4パターンのうちの共通している事になります。
だから、どれでやってくれても結局答えは変わらないです。
そして、大変さもそんなに変わらないです。
だから、どれでやってもいいかな、となってしまいがちですが、そこでまとめです。
一応つるかめ算は色んな解き方はもちろん出来ますが、おすすめは？とあえて聞かれるならばこの二つです。
式、要は二つ目の話です。
全体の差を1あたりの差で割るという計算で答えを求める事が出来るかどうかという事と、あとは表を使って答えを出す事が出来るか、というお話です。
式というのは単純で、別に図は書かなくてもこんな問題は答えが出るんだから式で書けた方がいいに決まっている。
そして、これは普通のつるかめ算ならそれだけでもいいですが、他の色んな解き方でもいいですが、式じゃないとどうしてもうまい事説明出来ない、例えば単位のややこしい速さのつるかめ算なんかはおそらく面積図とか表よりは式で計算した方が速いに決まっているという事になっています。
なので、その式の解き方に慣れるという事が結構大切だというお話があります。
もう1個の表解は何かと言いますと、それよりももうちょっと面倒くさい例えば今回は50円切手80円切手だけで終わりましたが、これが50円切手80円切手百十円切手と3種類が並んだ時にどうなるのかとか、合計金額が分かっている場合は別にいいんですが、例えば50円切手の代金と80円切手の代金の差が何百円でしたみたいな感じで、差を聞かれている、差のつるかめ算と言というケースもあります。
その場合は多分表解の方があっさり理解しやすいです。
逆に面積図だと何も出来なくなってしまうという事になってしまいます。
なので、二つ覚えろというのであればこの二つをちゃんと理解しておいてもらえるといいのかなと思います。
という事で、色んな解き方があって色んな考え方ももちろんありますが、おすすめとしてはまず式で単純なつるかめ算であればさっと計算出来るようになりましょうというのが一つ。
それから、複雑なものはまず1回表で書いてみましょう。
表で書き慣れるうちにだんだんだんだん表すらいらなくなってくるはずですので、まず表でこういう仕組みになっているんだという事を理解した状態でさらに練習を積み重ねていくという事をやってくれればいいかなと思っております。
中学受験における算数で文章題の正答率を上げるためのポイント
中学受験の算数において、文章題は必ず出題されます。文章題の正答率が上がる、安定して得点が取れるということは受験において非常に重要であると言えます。中学受験における算数で文章題の正答率を上げるためのポイントをおさえて文章題に取り組んでいきましょう。ここでは、文章題に対する取り組み方と、文章題を解くためのツールを例題とともに解説していきます。
文章を音読する
目だけで読むより、五感をなるべく多く使ったほうが脳が整理されて理解しやすくなります。
算数のなかでも文章題が苦手だと感じる場合は、特にひとつひとつの文を読み落とさずにしっかりと考えることを習慣づける必要があります。日頃から音読をしておくと、黙読したときでも音読したときと同じ位の理解の効果が得られるようになります。中学受験当日はもちろん声を出せないので、日ごろ積み重ねておくと文章を何度も読み直さなくても一度で文章題が理解できるようになります。
文章題に出てくる言葉の意味を理解する
中学受験の文章題には、さまざまな言葉がでてきます。「売上」「利益」「毎分」「静水時」「仕入れ値」など、文章の言葉を正しく理解できていないと計算するべきものが何なのか判断できなくなったり、そもそも文章が理解できずに不安になってしまい問題が解けないと思ってしまったりします。分からない言葉がでてきたときは、すぐに調べて覚えるようにしましょう。また、買い物に行ったときなどに、数字を見たり、重さを感じたり、体感できることはしておくと言葉の理解に苦しむことも少なくなります。
正確に文章を把握する
算数の文章題は、文章を読んで何が書かれているのか、何を問われているのかを正確に判断する必要があります。文章を読む段階で間違えた解釈をしてしまうと、そもそも答えにたどり着くことはできません。文章題の中には解き方のヒントが書かれている場合があります。
「ただし、〇〇とする」など、ただしが用いられている場合は、解答に必要な条件が書かれていることが多いです。自分の出した解答がただしで示された条件を活用しているか確認しましょう。
また、「たとえば」や、「例」が書かれている場合は、文章題の中の規則性、ルールなど、それより前に提示された条件の詳細を示しています。文章中に書かれているヒントを利用し、正答率を上げていきましょう。
文章を絵や図にする
文章題をそのまま文字として頭の中だけで理解しようとすることは難しく、中学受験の算数で出題される複雑な条件が提示された場合などは計算からはじめようとするとミスが起こりやすくなってしまいます。
文章題に書かれていることを線分図やベン図を用いてみたり、りんごを〇とするなど簡略化して絵を書いてみると、文章題がストーリーとして頭の中に描かれ、問題が解きやすくなります。絵で描けるということは、文章が理解できているということになります。そのまま数字だけで考えようとせずに、別の方法も用いて考えてみると計算しやすく、間違えにくくなります。
文章題を解くときに使用する主なツール
文章題を解くにあたって色々な問題を解くことは大切なことです。ここでは文章題を解くときに使う主なツールを挙げて、様々な角度から文章題を考えてみます。これらをしっかりと理解して問題に対して適切な解き方を選択し、活用できるようになりましょう。
線分図
●例題
しゅうじ君は初めに持っていたお金の３/４使い、次に残りのお金の１/３を使いました。すると、残金は400円になりました。しゅうじ君は、初めに何円持っていましたか。
●解き方
線分図を書いて解いていきましょう。
まず「全体を４つに分けたうちの３つ分を使い、次に残りのうちの３分の１を使ったので残金は400円になった」
ので、線分図で表すと右図のようになります。
400円が何□なのか考えてみると、
図より、400円＝̻2⃣であることが分かります。
400円＝2⃣なので、1⃣＝200円、3⃣＝600円となります。
そして、④から➂を引いた部分①と、
3⃣の線分図の長さは同じなので、3⃣＝600円＝①
はじめにしゅうじ君が持っていたのは④なので、
①＝600円より、600×４で 2400円が答えになります。
表
●例題
●解き方
表に整理して解いていきましょう。
48人の生徒にＡ、Ｂ２問のテストをしたところ、
Ａができた人は15人、Ｂができた人は27人、
両方できた人と１問もできなかった人の人数の比が
３：５なので➂、⑤とすると、右のような表を書くことができます。
そして、
48人のうちＡができなかった人の人数が15人なので、
Ａができなかった人の人数は、48-15＝33 で、33人
Ｂができなかった人の人数は、48-27＝21で、22人
ということが分かります。
つぎに、このような問題の解き方としてポイントなのが
必ず、何か分からないときは記号を１つ作ってその記号に関する式を立ててみましょう。
ここでは☆として考えていきます。そうすると、
➂＋☆＝27人、⑤＋☆＝33人
という式が立てられます。
ちがいに注目すると、②＝６人なので、➂＝９人、
Ａができた人の人数15人からＡもＢもどちらもできた人の人数9人を引いて
15-９＝６人がＡだけできた人の人数になります。
てんびん
●例題
●解き方
てんびん算で解いていきます。
まず、食塩10%、170ｇの食塩水と、食塩を○ｇ加えると15％の食塩水になるので
図に表すと右のようになります。
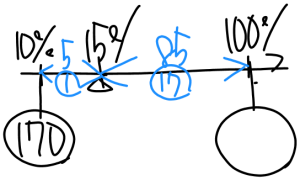
次にてんびんのうでの長さに注目します。
15％と10％は５％離れていて、
100％と15％は85％離れているので、
比に直すと １：17 となります。
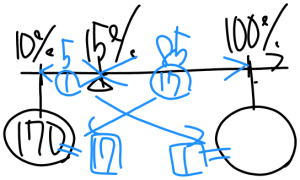
うでの長さの比と重さの比は逆算になっているので
17：１であることが分かります。
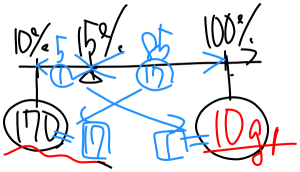
□17が170なので、1⃣＝10となり、
10gが答えとなります。
ベン図
●例題
●解き方
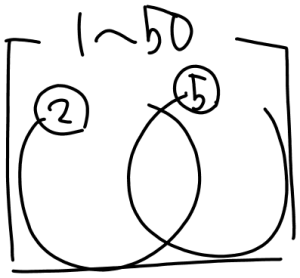
ベン図を用いて解いていきます。
まず問題文を図に表すと右のようになります。
１から50までに
２の倍数は50÷２＝25で25個、
５の倍数は50÷５＝10で10個 だとわかります。
また、円が重なっているところに注目します。
２と５で割り切れるということは、
２と５の最小公倍数は10なので、
50÷10＝５ で、図のようになります。
また、
25個のうち重なっているところが10個あるので
25－10＝15
10個のうち重なっているところが５個あるので
10-5＝５となります。
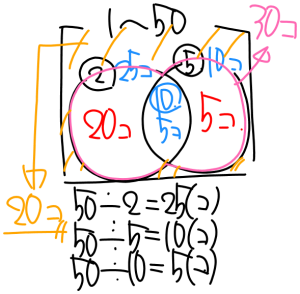１~50のうち、２と５どちらかで割り切れる数は
20＋5＋5＝30 で30個あることがわかります。
２でも５でも割り切れない数を求めたいので
ベン図の外側の部分を求めます。
50－30＝20 20個が答えとなります。
概念図
●例題
何人かの子どもに折り紙を配ります。１人に４枚ずつ配ると29枚余り、１人に６枚ずつ配ると５枚余ります。子どもは何人いますか。
●解き方
この問題は過不足算、差集め算の問題です。
概念図を用いて解いていきます。
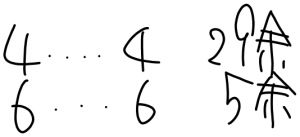
１人に４枚ずつ配ると29枚余る、
１人に６枚ずつ配ると５枚余るので
右のようになります。
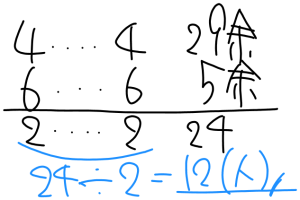１人あたりの差がどれくらいなのか
全体としての差がどれくらいなのかを見ていきます。
１人あたりの差は６－４＝２で
１人２枚ずつ差があり、
全体としての差は29－５＝24で24枚
となるので、全体÷１人あたりの枚数
24÷２＝12人となります。
まとめ
当塾では完全１対１の個別指導で、文章題の問題を徹底的にマスターしたり、算数の苦手を克服したりと完全オーダーメイドの授業でひとりひとりに合わせた授業を行っております。夏井塾独自の授業システムについてはぜひこちらをご覧ください。また、教室で受ける授業をオンラインでも受講可能です。中学受験算数の成績を「オンライン個別指導」で伸ばすことができる３つの理由でもあるように、通塾の時間も必要なく、体力を温存したまま勉強しなれた環境でより集中して授業に取り組むことができます。
算数の文章題は、少し意識を変えるだけで格段に解きやすくなります。中学受験の算数で文章題の正答率を上げるためには、文章題を正しく読み解くということを常に意識して問題演習に取り組みましょう。
関連記事
・中学受験算数の比の文章題
・中学受験における算数、文章題の勉強法
・中学受験算数における様々な種類の文章題対策
