中学受験 算数の文章題が苦手な子へ｜つるかめ算・割合・並べ方の読み方と解き方
このページでは、上の動画で解説している「つるかめ算の基本と複数の解き方」を中心に、中学受験の算数で文章題の正答率を上げるコツや、文章題を解くときに役立つ代表的な図・表のツールをまとめて紹介します。
つるかめ算は、和差算に続いて頻出の文章題単元であり、解き方も複数存在する重要テーマです。ここで整理しておくことで、他の文章題にも応用できる「考え方の型」が身についていきます。
つるかめ算の基本と複数の解き方
つるかめ算とは？
今回は単元別のコツということで、つるかめ算について解説します。つるかめ算は、文章題の中でも登場頻度が高く、いわゆる文章題の中では和差算に続いてよく扱われる単元です。
- 多くの生徒がすでに学習したことのある内容
- 問題のパターンが多く、応用問題にもつながる単元
- 解き方が複数あるのが大きな特徴
シンプルな問題であっても、実は色々なアプローチができる点がポイントです。
例題：50円切手と80円切手の問題
代表的なつるかめ算の例として、次のような問題を考えてみましょう。
50円切手と、最近あまり見かけなくなりましたが、80円切手があります。
合計で20枚あり、その合計金額が1240円になりました。
では、50円切手と80円切手はそれぞれ何枚あるでしょうか？
これが、いわゆるつるかめ算と呼ばれる文章題です。
つるかめ算には、有名な解き方だけでもざっと5パターンほど存在します。
- よく使われるメジャーな方法
- あまり見たことがないニッチな方法
ここでは代表的な解き方を整理しながら、それぞれの考え方を確認していきます。
解法１：面積図を使った解き方
もっともよく使われるのは、面積図を使った解き方です。これは、「金額＝価格×枚数」を「面積」として表して考える方法です。
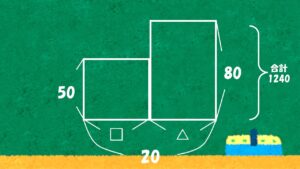
- 50円切手：縦を50円、横を枚数（分からないので□）で表す
- 80円切手：縦を80円、横を枚数（同じく□）で表す
すると、それぞれの面積が、そのまま金額（＝価格 × 枚数）を表すことになります。これが、いわゆる面積図による解法です。
問題より、
- 合計金額は 1240円
- 枚数の合計は 20枚
ですから、
- 2つの面積（＝金額）を足すと 1240円
- 横の長さ（＝枚数）を足すと 20枚
という条件が図で表せます。
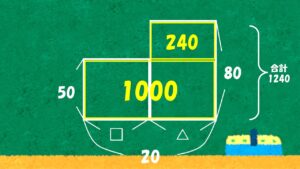
図をよく見ると、例えば下の部分（すべて50円切手の場合）の金額は、
- 縦が50、横が20なので、50×20＝1000円
となります。実際の合計は1240円なので、
- 上側の面積（＝80円切手部分）は 1240－1000＝240円
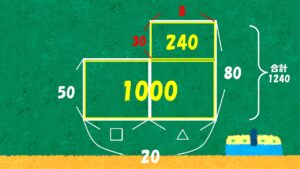
さらに、縦の長さに注目すると、
- 80円と50円の差は 30円
なので、
- 240 ÷ 30 ＝ 8枚 … 80円切手の枚数
- 20 － 8 ＝ 12枚 … 50円切手の枚数
というようにして答えが求まります。これが面積図を使ったつるかめ算の解き方です。
解法２：式（全体の差 ÷ 1あたりの差）で解く方法
次は、図を使わず式だけで解く方法です。考え方は面積図と同じですが、「全体の差を1あたりの差で割る」という形に整理します。
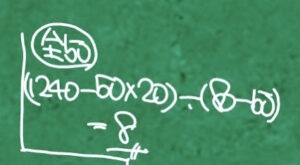
80円切手の枚数を求めたいとき、次のように考えます。
- もし全部が50円切手だったらどうなるかを考える（これを「全50」と呼ぶこともあります）。
- 50円切手が20枚 ⇒ 50×20＝1000円
- しかし実際の合計は 1240円なので、全体の差は 240円
- 1枚あたりの差は 80－50＝30円
- よって、全体の差 ÷ 1あたりの差＝240 ÷ 30＝8枚（80円切手の枚数）
- 残りは 20－8＝12枚（50円切手の枚数）
さきほどの面積図の答えと完全に一致しますが、図を書かずに式だけで完結できるのがこの方法の利点です。
解法３：表解で考える方法
同じ問題を、表に整理して考える方法もよく使われます。
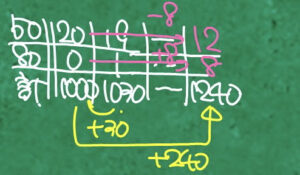
- まず、「全部50円切手」のケース（20枚・0枚）からスタートする。
50×20＝1000円、80×0＝0円 ⇒ 合計1000円。 - 実際は1240円なので「まだ足りない」と分かる。
- 次に「19枚・1枚」のケースを考える。
50×19＝950円、80×1＝80円 ⇒ 合計1030円。 - 1回交換するごとに金額が30円ずつ増えていくことに気づく。
- 240円増やすには、240 ÷ 30＝8回交換が必要。
- 20枚あった50円切手から8枚が80円切手に変わるので、
50円切手：20－8＝12枚、80円切手：0＋8＝8枚。
このように、「1回交換するごとにいくら変わるか」を表で追いかけていくのが表解です。
解法４：状況図（差に注目する図）で解く方法
次は、いわゆる状況図を使った解き方です。考え方は「全50」の式解法と似ており、差集め算・過不足算に近い発想で解きます。
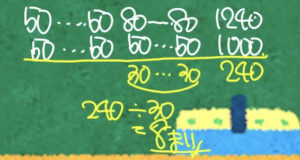
- 50円切手と80円切手が何枚かずつあって、枚数は20枚、合計金額は1240円。
- 「もし全部が50円切手だったら？」と考えると、合計は 50×20＝1000円。
- 実際は1240円なので、合計金額の差は 240円。
- 1枚あたりの差は 80－50＝30円なので、1枚につき30円の差が生まれている。
- 240 ÷ 30＝8枚 ⇒ もともと80円切手だったものが8枚。
このように、「全体の差」と「1枚あたりの差」に注目して図で整理するのが状況図の解き方です。
どの解き方を覚えるべきか？おすすめはこの２つ
ここまで4つの解き方を見てきましたが、実はどの方法でも
- 出てくる数字はすべて同じ
- 計算内容もまったく同じ
であり、違うのは「表現の仕方」だけです。つまり、
- どの方法で解いても答えは変わらない
- 計算の大変さも大きくは変わらない
とはいえ、「どれを中心に身につけるべきか？」と聞かれたときのおすすめは次の２つです。
- 式（全体の差 ÷ 1あたりの差）の解法
単純なつるかめ算であれば、図を書かなくても式だけで答えが出せるので、スピードと汎用性が高い方法です。
とくに、単位がややこしい速さのつるかめ算などは、面積図や表よりも式で整理した方が速いケースが多くなります。 - 表解
条件が増えたとき（例：50円・80円・110円の3種類、差が条件に出てくる「差のつるかめ算」など）は、表に書き出した方が構造を理解しやすいです。
面積図では扱いづらい場合でも、表解ならスムーズに整理できる問題が多くなります。
まずは、
- 簡単なつるかめ算は「式」でサッと解けるようになる
- 複雑な条件の問題は、まず「表」で整理してみる
という２本柱を意識しておくと、つるかめ算全体への対応力が一気に高まります。表で慣れてくると、そのうち表を書かなくても頭の中で整理できるようになっていきます。
中学受験の算数で文章題の正答率を上げるポイント
中学受験の算数では、文章題は必ず出題されます。文章題の正答率が安定していること＝得点の安定に直結するといっても過言ではありません。
ここでは、文章題に対する基本的な取り組み方と、得点力を上げるためのポイントを整理します。
１．文章を音読する
目だけで読むより、五感をなるべく多く使ったほうが、脳が整理されて理解しやすくなります。
- 文章題が苦手な場合ほど、一文一文を読み落とさずに丁寧に読む習慣が大切
- 日頃から音読をしておくと、黙読でも音読と同じレベルの理解ができるようになる
- 入試本番では声を出せないため、普段からの積み重ねが重要
音読の習慣が身につくと、文章を何度も読み直さなくても、一度で内容が頭に入るようになり、読み間違い・条件の取りこぼしが減っていきます。
２．文章題に出てくる言葉の意味を理解する
中学受験の文章題には、さまざまな用語が登場します。
- 売上・利益・仕入れ値
- 毎分・毎時・静水時
- 割合・濃度・速さ など
これらの言葉を正しく理解できていないと、
- 「何を求めればよいのか」が分からない
- 文章自体が理解できず、不安になって手が止まる
といった状態になりやすくなります。
分からない言葉が出てきたときは、その場で調べて覚えることが大切です。また、買い物や料理など日常生活の中で、実際に「重さ」「値段」「時間」を体感しておくと、言葉のイメージがつかみやすくなります。
３．正確に文章を把握する
算数の文章題では、
- 何が書かれているのか（条件）
- 何を問われているのか（ゴール）
を正確に読み取る必要があります。ここで読み違えると、どんなに計算ができても正答にはたどり着けません。
文章題の中には解き方のヒントが書かれていることが多くあります。
- 「ただし、〇〇とする」
⇒ 解答に必要な条件が書かれていることが多いので、必ずチェック。 - 「たとえば」や「例」
⇒ それ以前に出てきた条件の具体例・規則性を示していることが多い。
自分の立てた式や出した答えが、これらのヒントときちんと対応しているか確認する習慣をつけることで、正答率が上がっていきます。
４．文章を絵や図にする
文章だけを頭の中で処理しようとすると、複雑な条件が出てきたときに混乱しやすくなります。そこで有効なのが、
- 線分図・ベン図・表・概念図・てんびん図などを使って、文章を「見える形」にすること
- りんごを〇、男の子を△など、簡単な絵や記号で置き換えること
絵や図で表せるということは、文章の内容を理解できているということでもあります。数字だけで考えようとせず、図や表も積極的に使っていきましょう。
文章題を解くときに使う主なツールと例題
文章題を解くうえで、ただ問題数をこなすだけでなく、状況を整理するためのツールを使い分けることが重要です。ここでは、代表的なツールとその例題・解き方を紹介します。
１．線分図
●例題
●解き方
線分図を書いて、全体と残り・使った分の関係を整理します。
- 「全体を4つに分けたうちの3つ分を使い、残り1つが残る」
- さらに「残りの3分の1を使って、残金が400円になった」と考える
これを線分図に表すと、右図のように「いくつ分＝400円なのか」が読み取りやすくなります。
図より、
- 400円が「2⃣」に相当することが分かる
- 400円＝2⃣ ⇒ 1⃣＝200円
- 3⃣＝600円 となる
さらに、
- 「④」から「③」を引いた部分①と、3⃣の長さは同じ ⇒ 3⃣＝600円＝①
- はじめに持っていたお金は④なので、600円×4＝2400円
線分図を使うことで、割合の関係が視覚的に整理できるのがポイントです。
２．表
●例題
●解き方
まず、情報を表に整理します。
- Ａができた人：15人
- Ｂができた人：27人
- 両方できた人と、どちらもできなかった人の比：3：5 ⇒ ➂、⑤ とおく
次に、
- Ａができなかった人：48－15＝33人
- Ｂができなかった人：48－27＝21人
「分からない部分」は記号（ここでは☆）を使って式を立てます。
- ➂＋☆＝27人
- ⑤＋☆＝33人
差に注目すると、
- ②＝6人 ⇒ ➂＝9人
- Ａができた人 15人から、ＡもＢもできた人9人を引くと、Aだけできた人は 15－9＝6人
このように、表を使うことで条件の整理・式立ての流れが見えやすくなります。
３．てんびん
●例題
●解き方
てんびん図を使って、濃度と重さの関係を整理します。
- 10％の食塩水 170g
- 食塩そのもの 100％
- 混ぜた結果が 15％
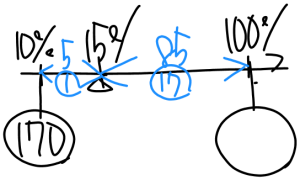
てんびんの腕の長さに注目すると、
- 15％と10％の差：5％
- 100％と15％の差：85％
- よって比は 1：17
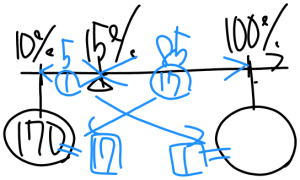
てんびんの場合、腕の長さの比と重さの比は逆比になります。
- 重さの比は 17：1
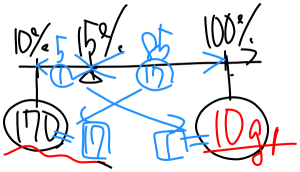
170gが□17にあたるので、
- 1⃣＝10g ⇒ 食塩は 10g 加えればよい
４．ベン図
●例題
●解き方
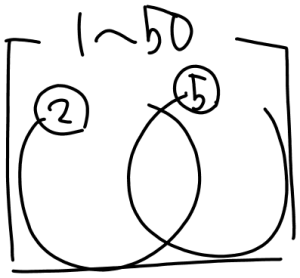
条件をベン図で整理します。
- 円A：2の倍数
- 円B：5の倍数
- 全体：1〜50の整数
- 2の倍数：50÷2＝25個
- 5の倍数：50÷5＝10個
- 2と5の最小公倍数は10 ⇒ 両方の倍数は 50÷10＝5個
- 2の倍数のうち、5の倍数と重なる部分5個を除くと、25－5＝20個
- 5の倍数のうち、2の倍数と重なる部分5個を除くと、10－5＝5個
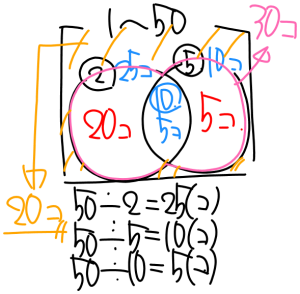
1〜50のうち、2または5どちらかで割り切れる数は、
- 20＋5＋5＝30個
したがって、2でも5でも割り切れない数は、
- 50－30＝20個
５．概念図
●例題
●解き方
この問題はいわゆる過不足算・差集め算のタイプで、概念図を使うと整理しやすくなります。
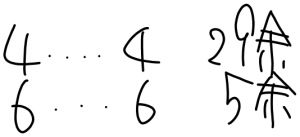
- 1人に4枚ずつ配ると29枚余る
- 1人に6枚ずつ配ると5枚余る
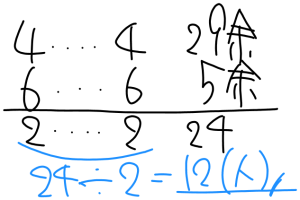
1人あたりの差・全体の差に注目します。
- 1人あたりの差：6－4＝2枚
- 全体の差：29－5＝24枚
したがって、
- 24÷2＝12人 … 子どもの人数
まとめ
当塾では、完全１対１の個別指導で、
- 文章題のさまざまなパターンを徹底的にマスターしたい
- 算数の苦手を克服したい
- 自分のペースでじっくり理解を深めたい
といったお子さま一人ひとりに合わせた授業を行っています。夏井塾独自の授業システムについては、ぜひこちらもご覧ください。
また、教室で受ける授業をオンラインでも受講可能です。中学受験算数の成績を「オンライン個別指導」で伸ばすことができる３つの理由でも紹介している通り、通塾時間が不要になり、体力を温存した状態で、慣れた環境から集中して学習に取り組むことができます。
算数の文章題は、少し意識を変えるだけで格段に解きやすくなります。
中学受験の算数で文章題の正答率を上げるためには、文章題を正しく読み解くということを常に意識して問題演習に取り組んでいきましょう。
関連記事
