中学受験算数で場合の数を取りきるための解き方
今回は単元別のコツ、場合の数という事で、普段授業の中ではあまり扱えない、
あまり説明が出来ない、もちろん説明はしますがさっと素通りしてしまうような話ではあるんですが意外と大事な事がこの算数を勉強する中では多かったりします。
そんな事をちょっと順番にお話し出来ればなと思っております。
という訳でまず、場合の数という事ですが、場合の数は結構広い単元になっています。
色んな問題が含まれているな、という事になっていますが基本的にこの場合の数の単元は嫌われやすいです。
場合の数が得意だ、と言っている生徒さんの10倍ぐらい場合の数は苦手だ、と言っている生徒さんが多いなというのが正直な印象になります。
なので、まずこのなぜ場合の数は嫌われるのか、という事になります。
色々解いている様子だったり理解するステップを確認していくと、明らかにこれだろうな、というのがまず1個挙げられます。
それが何かと言いますと、問題の種類がめちゃくちゃ多いです。
例えば、カードを並べるという問題一つとったとしても、それが1、2、3、4、5の場合と0、1、2、3、4というふうにカードの数字が違うだけで問題が変わってしまう事が多かったりします。
さらに、これが0、1、1、2、3みたいな感じで同じカードが複数枚あるとまた解き方が変わってしまうという事で、ぱっと見一見同じような問題に見えるのに全然違う問題になっているという事が結構多いからという事になります。
そしてカードに限らず色んな問題があります。
道順の問題もそうです。
色の塗り分けの問題もそうです。
それから順番に並べるというような問題もそうです。
並べ方で終わるかと思ったら今度は選び方の話が出てきます。
という事で、色んな話がごちゃごちゃに登場するというのが場合の数の単元になります。
しかもそれを結構1回なり2回の授業で一気にガッーとやってしまうという塾も結構多いかと思います。
ですので、覚える事も多いし、感じる事も多いし、引っ掛かるポイントもたくさんあるという事で、だんだん点数が取れなくなってきて凄く嫌いだなと思う生徒さんは非常に多いなというのが正直な所です。
じゃあ、どうしていったらいいんだろうかという事になります。
もちろんその全部をしっかりと覚えて、全部をしっかり解けるようにする練習をするという事はもちろん大事ですが、そもそも何が大事で何が大事じゃないのかという事をちゃんと見極める事は非常に大切なのかなと思っています。
一番大事なことは?
やはり場合の数の根本に当たる部分がしっかり理解出来ているかどうか、という所になります。
それは何かと言いますと、積の法則と和の法則という二つの法則があります。
もちろんこれは、場合の数の問題を解く時に必ず使う考え方なので、なんとなくは理解している生徒さんは非常に多いです。
しかし、それをちゃんと分けてしっかり理解しているという生徒さんは意外と少なかったりします。
しかも何が面倒臭いかというと、説明が難しいです。
はっきりとこれが積の法則だ、これが和の法則だと言えるんですが、じゃあこれどっちなの?と言われた時に結構困る事が多かったりします。
例えば、0、1、2、3、4という5枚のカードがあって、これで三桁の整数のうち三桁の偶数は何通り出来るんですか?みたいな問題が仮にあったとしましょう。
これがちょうど積の法則と和の法則を両方とも使う問題になるので結構勉強になるかな、という所です。
まずこういう問題を考える時には、偶数だと言っていますのでもちろん一の位に注目する訳です。
0、1、2、3、4という数を使って偶数を作ろうかなと思った場合、それは一の位が0の場合と一の位が2の場合と4の場合という3パターン考えられるという事になるというお話になります。
それぞれ場合の数が何通りあるかな、という事を考える事になる訳ですが、最初に0を使った場合を考えます。
0を使った場合は、残りのカード1、2、3、4をご自由にここに放り込んでいいですよ、という事になっています。
ですので、順番に計算する時には百の位から順番に決めていく訳です。
百の位の場合はもちろん1、2、3、4をなんでもいいから4通りになるという事が分かります。
そして次の十の位は1枚減っていますから3通りだという事が分かります。
という事で、4×3=12通りあるな、という事が分かればいいという事になります。
そして、他方一の位が2の場合4の場合はちょっと話が変わってきます。
一の位が2だった場合は百の位には0が入らないという条件が入っています。
つまり、百の位を今から考えようかなと思ったらもちろん2は使えませんし0も使えないという事になっています。
なので、ここの百の位は3通りの選び方があるよね、という事になっています。
十の位はさっきと変わりません。
結局残り3枚のうちから好きなものを選んで下さいという事になるので3通りという事になるよね、という事になります。
これが9通りだという事になっています。
4の場合も一緒です。
百の位が3通りで十の位が3通りあるよね、という事になるので、9通りあるという事が分かるという事になります。
という事で、今さらっと何をやったかというと、百の位の選び方と十の位の選び方を決めてあげる事で、この三桁の偶数の作り方がそれぞれ12通り、9通り、9通りあったよという事です。
これはそれぞれの位を考えて、今求めたいのは三桁の数の話をしてる訳ですから掛け算で求める事になります。
これが積の法則と言われるものです。
じゃあ、和の法則とは何かというと、12、9、9と出てきた時に、じゃあ最後結局答えが何通りですか?と言われて、よく12×9×9だ!という生徒さんは結構多いです。
ですが、もちろんこれは理解出来ている人には当たり前の話ですが、足します。
12+9+9だから答えは30通りという事になります。
という事で、これが和の法則と言われるものです。
これが掛けるのか足すのかという区別がつかない生徒さんが結構多かったりします。
一応授業ではこういうふうに言います。
それぞれの部分部分を考える時は積の法則を考えましょう。
そして12、9、9というのは三桁の偶数が12個ある、9個ある、9個あると言っています。
これでもう完成してしまっているので、これは掛けずに足してあげましょうというふうな区別をしてくれればいいという事になります。
この説明だけで分かるかというともちろんそういう訳ではないです。
ここから練習していって、これが掛けるタイミングだ、これが足すタイミングだとなんとなく理解した結果、なんとなく答えが出るようになるという事でステップを踏んであげないと中々うまくならないという事があったりします。
なので、これについては練習が必要ですが一応概念としてはこんな感じになっています。
この区別がちゃんとつくかどうかで、この場合の数の問題が得意になるかならないかというのが結構変わってきますので、これはぜひ注意して欲しいなと思います。
そしてもう1個が場合分けです。
今サラッとやりましたが、これもそうです。
偶数だという事は、一の位が0の場合と2の場合と4の場合もあります。
それ以外は何もないよね、という状態までちゃんと分ける事が出来るかどうかというのが結構大事です。
場合分けの仕方を間違えるととんでもない事になります。
これも実際に生徒さんでよくやりますが、じゃあまずは百何十何で偶数になるものを考えよう、次は二百の場合を考えよう、三百の場合考えようとやると、もう訳分からなくなります。
場合分けの仕方を間違えるだけで問題が極端に難しくなってしまいます。
という事になるので、場合分けをマスターするという事はとても大事です。
場合分けさえ間違えなければ、実はもの凄く簡単に場合の数の問題は計算出来るんだ、というのがよく言われる話であります。
なので、そこをしっかり意識して考えましょう。
要は、今からこの問題を解こうとした時に、じゃあこの言われている問題は一体どういうパターンに分ける事が出来るだろうか、という事を考えましょうという事です。
これは場合の数の問題で考える時も必要ですし、その他の問題を考える時ももちろん大事です。
例えば、速さの問題を考える時に前に進んでいる場合と後に進んでいる場合の2パターンあるよねとか、あとは商売の問題、売買損益の問題を考える時に得している場合それから損している場合これ2パターンあるよねとか、色んなパターン分けというのはあったりする訳です。
これは場合の数に限った話ではないですが、それをちゃんとうまく分ける事が出来るかどうかというのは非常に算数の問題を考える上でとても大切なお話ではあります。
なので、そこら辺をしっかりと意識しながら勉強を進めていくという事で場合の数がちょっとずつ得意になってくるといいんじゃないかなと思います。

夏井算数塾の『個別オンライン指導』:自宅で楽しく学べる!
中学受験算数で場合の数を取りきるための解き方
ある条件が起こる場合、それが何通りあるのかを求めるのが「場合の数」です。中学受験の算数において場合の数は非常に多く出題される単元です。いろいろな解き方を知ったうえで、問題に合わせて解き方を選びながら解いていく必要があります。確実に点数をとれるように解き方と使い方をしっかりと理解しておきましょう。
樹形図を用いる
中学受験の算数は、計算ではなく書き出すことができれば解ける問題が多く、樹形図を用いることで効率的に答えを導くことができます。「順列」、「組み合わせ」は計算で解くこともできますが、樹形図で求めることもできます。樹形図を書くときには、問題文に書かれている順番に従って書くようにしましょう。また、「〇人の中から△人を選ぶ」といった問題の場合は、ABCなど自分が分かりやすい名前を付けて樹形図を書きましょう。樹形図を書くと数字だけでは分かりにくかった部分が視覚で判断できるので、問題が解きやすくなります。
受験本番では、1問にかけられる時間が少ないため、計算を使って解いた方がはやく解ける場合は計算を用いるようにしましょう。ただし、計算だけに頼り切ってしまうと思考力を必要とする問題が解けないということになります。日々の勉強の中で樹形図を書くようにすることで思考力を身につけるということを怠らないようにしましょう。
場合分けの重要性について
場合分けの問題を解くとき、どの視点で場合分けをするのかを見極める必要があります。間違った視点に立ってしまうと、考えなくてもいい可能性についてまで考えてしまったりと必要のない時間を費やしてしまうことになります。また、問題を解いている最中に答えるべきことを見失ってしまうこともあるので、解いた後は見直しをしましょう。問題で問われている内容をきちんと理解し、正しい視点に立って場合分けをすることが大切です。
余事象を考える
たとえば0を含むカード数枚から偶数となる場合を求めるとき、偶数を求めようとするのではなく、全体から奇数を引いた方が答えをはやく出すことができます。もちろん偶数を求めようとしても答えを出すことはできますが、全体から奇数を引いた計算をする場合よりも、時間がかかってしまいます。余事象を使って解ける問題はうまく活用していきましょう。中学受験は時間とのたたかいです。解答を導くための最短ルートを常に探しながら問題を解くようにしましょう。

夏井算数塾の『個別オンライン指導』:自宅で楽しく学べる!
場合の数の問題演習
●例題
(2) 【7】、【8】、【9】、【0】の4枚のカードのうち、3枚を並べて3けたの奇数をつくる。
(3) 【A】、【B】、【C】、【D】の4枚のカードを【A】と【B】がいつもとなり合うように1列に並べる。
●解き方
●例題
●解き方
●例題
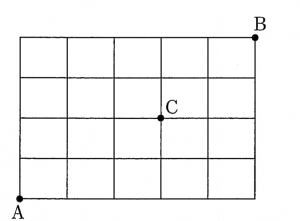
●解き方

Aから遠回りせずに途中でCを通る道順なので、
青い線のところしか通ることが出来ません。

AからCまで遠回りせずにCまで行くときの道順を
考えてみると10通りあるということが分かります。

次にCからBまで遠回りせずに行くときの道順を考えます。
AからCまでに行くために10通りあるということは、
左の図のようになります。
30通り+30通りで60通りが答えとなります。
まとめ
場合の数は計算で答えを出すことができる問題が多いですが、計算だけで解き切ろうとすると、それだけでは解けない問題に直面した時にどう考えれば良いのか分からず、後々苦戦してしまうことになります。計算で解く際にもなぜそうなるのか?を常に考えながら問題を解いていくことが必要です。中学受験算数で場合の数の問題を取りきるためには、日々の問題演習の中で思考力を身につけながら学習を進めていきましょう。
当塾での取り組み
当塾では完全個別の1対1の授業で、場合の数の問題の苦手克服のための授業が受講できます。当塾の授業の独自のシステムついては夏井算数塾・個別指導はココが違う!をご覧ください。また、教室での授業と同様の授業をオンラインでも受講可能です。通塾の必要がなく、全国どこからでも勉強しなれた環境で受講可能で、勉強だけに集中して取り組むことができます。詳細は今までにない、”業界初”のオンライン算数個別指導「ウィズ・ユー」をご覧ください。



